
Asal Sayıların Tarihçesi Nedir?
Asal sayılar, matematiğin temel unsurlarından biridir ve yalnızca 1 ile kendisine bölünebilen pozitif tam sayılardır. Bu yazıda asal sayıların tarihçesi, keşifleri ve matematikteki önemi ele alınmaktadır. Asal sayıların keşfi, antik dönemlerden modern çağa kadar uzanan bir yolculuğu temsil eder.
Asal sayılar, matematiğin en temel unsurlarından biri olarak kabul edilir. Bir asal sayı, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan bir tam sayıdır. Matematiksel anlamda asal sayılar, sayı teorisinin temel taşlarını oluşturur ve tarih boyunca birçok bilim insanı ve matematikçi tarafından incelenmiştir. Bu makalede, asal sayıların tarihçesi, keşifleri ve matematikteki önemi ele alınacaktır. Asal Sayıların Keşfi Asal sayıların tarihçesi, antik dönemlere kadar uzanmaktadır. Eski Yunan matematikçileri, özellikle Euclid, asal sayıların özelliklerini incelemiş ve sayılar arasındaki ilişkileri tanımlamıştır. Euclid, "Asal Sayıların Sonsuzluğu" teoremi ile asal sayıların sayısının sonlu olmadığını kanıtlamıştır.
Orta Çağ ve Rönesans Dönemi Orta Çağ boyunca, matematiksel çalışmaların büyük bir kısmı İslam dünyasında gerçekleştirilmiştir. Bu dönemde matematikçiler, asal sayılarla ilgili çeşitli teoriler geliştirmiştir. Özellikle, Arap matematikçi Al-Khwarizmi, asal sayıların özellikleri üzerine önemli eserler bırakmıştır. Rönesans döneminde ise, asal sayılar üzerine yapılan çalışmalar devam etmiş ve bu sayılar, sayı teorisi alanında daha fazla ilgi görmeye başlamıştır. Modern Dönemde Asal Sayılar 19. yüzyılın sonlarına doğru, asal sayılar üzerine daha sistematik bir şekilde çalışmalar yapılmaya başlanmıştır. Matematikçiler, asal sayılar ile ilgili çeşitli hipotezler ve teoremler geliştirmiştir. Örneğin, "Asal Sayılar Teoremi", asal sayıların dağılımını belirleyen önemli bir sonuçtur.
Asal Sayıların Kriptografideki Rolü Günümüzde, asal sayılar bilgisayar bilimi ve kriptografi alanında vazgeçilmez bir yere sahiptir. Özellikle RSA algoritması, büyük asal sayıların çarpanlarına ayrılması prensibi üzerine kurulmuştur. Bu durum, asal sayıların güvenlik sistemlerinde neden bu kadar önemli olduğunu gösterir.
Sonuç Sonuç olarak, asal sayılar tarihi, matematiksel düşüncenin evrimi ve insanlık tarihinin önemli bir parçasını temsil eder. Asal sayıların keşfi, tarih boyunca birçok matematikçi için ilham kaynağı olmuştur. Modern çağda ise, asal sayılar, sadece teorik bir konu olmanın ötesinde, günlük yaşamda ve teknolojide önemli bir rol oynamaktadır. Bu nedenle, asal sayıların tarihçesi, matematiksel araştırmaların yanı sıra, bilim ve teknolojideki gelişmeler için de kritik bir öneme sahiptir. |
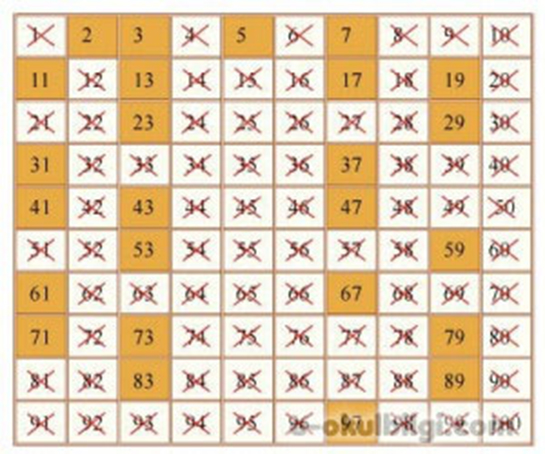
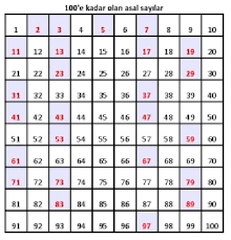

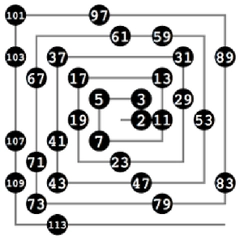





Güzel bilgi topladım teşekkür ediyorum inşallah güzel bir not alırım.
Rica ederim Elif hanım, umarım emeğinizin karşılığını alır ve güzel bir not alırsınız. Başarılar dilerim!