Bu içerik, asal sayıların tanımını ve 0 sayısının asal sayı olup olmadığını ele alıyor. Asal sayıların yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılar olduğu belirtiliyor. 0 sayısının bu tanıma uymadığı ve dolayısıyla asal sayı olmadığı açıklanıyor. Matematiksel kuralların önemine vurgu yapılıyor.
Merak ettiğiniz konular hakkında hızlı ve güvenilir bilgilere ulaşabilmeniz için bu sayfayı oluşturduk. Aşağıda, yayınladığımız içerikleri ve diğer konularla ilgili en sık sorulan soruların cevaplarını bulabilirsiniz. Eğer burada yanıtını bulamadığınız bir sorunuz varsa, lütfen bizimle iletişime geçin. Size en kısa sürede geri dönüş yapacağız ve sorularınızı yanıtlamaktan mutluluk duyacağız.
0 Asal Sayı mıdır?
0 ile her sayı aralarında asal mıdır?
Matematikte aralarında asal kavramı, iki sayının 1'den büyük ortak böleni olmaması durumunu ifade eder. Ancak sıfır sayısı bu tanımda özel bir konuma sahiptir ve diğer sayılarla olan ilişkisi farklı matematiksel kurallara dayanır.
1'den 100'e Kadar Asal Sayılar Nelerdir?
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan sayılardır. Matematikteki temel kavramlardan biri olan asal sayılar, birçok teorinin ve uygulamanın temelini oluşturur. Bu içerikte, 1'den 100'e kadar olan asal sayılar, özellikleri ve tarihçesi ele alınmaktadır.
1 her sayıyla aralarında asal mıdır?
Matematikte 1'in diğer sayılarla olan ilişkisi, aralarında asallık kavramı üzerinden incelenir. Bu durum, sayılar teorisindeki temel tanımlar ve 1'in benzersiz özellikleriyle açıklanır.
1 ile her sayı aralarında asal mıdır?
Matematikteki temel kavramlardan biri olan aralarında asallık ilişkisi, 1 sayısı özelinde ilginç bir durum ortaya koyuyor. Sayılar teorisinde önemli bir yere sahip bu ilişki, 1'in diğer tüm sayılarla olan bağlantısını tanımlayan matematiksel bir gerçeği ifade ediyor.
1 ile herhangi bir sayı aralarında asal mıdır?
Matematikteki temel kurallardan biri, 1'in tüm tam sayılarla aralarında asal olmasıdır. Bu durum, aralarında asallık tanımı ve 1'in benzersiz matematiksel özellikleriyle açıklanır. En büyük ortak bölenin daima 1 olması, bu ilişkinin evrensel bir gerçek olduğunu gösterir.
1 Neden Asal Sayı Değildir?
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Bu makalede, asal sayı olma tanımını karşılamayan sayıların özellikleri ve örneklerle açıklamaları ele alınacaktır. Asal olmayan sayılar arasındaki temel farklar ve bu durumun matematiksel önemi vurgulanacaktır.
1 ve 1 aralarında asal mıdır?
İki sayının aralarında asal olması için EBOB değerinin 1 olması gerektiği temel kuralı, 1 ve 1 özelinde ilginç bir durum ortaya koyuyor. Bu durum matematiksel tanımla pratik kullanım arasındaki ince ayrımları gözler önüne seriyor.
10 tane asal çarpan örneği verebilir misiniz?
Sayıların temel yapı taşlarını oluşturan asal çarpanlar, matematiksel işlemlerin anlaşılmasında önemli bir rol oynar. Farklı sayıların asal çarpanlarına ayrılmış halleri, bu sayıların iç yapısını ve birbirleriyle olan ilişkilerini gözlemlememizi sağlar.
100'e kadar olan asal sayılar hangileridir?
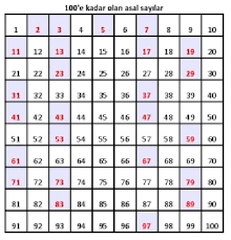
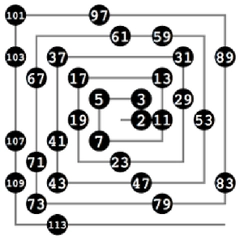
Matematik dünyasının yapı taşları olan asal sayılar, 100'e kadar olan aralıkta belirli bir düzen içinde sıralanır. Bu özel sayı grubu, yalnızca kendisi ve 1'e bölünebilme özelliğiyle diğer sayılardan ayrılır. Aritmetiğin temelini oluşturan bu sayıların listesi ve temel özellikleri aşağıda sunulmuştur.
100'e kadar 17 ile aralarında asal olan sayılar hangileridir?
Aralarında asal sayılar, 1'den başka ortak böleni olmayan sayı çiftlerini ifade eder. 17 asal bir sayı olduğundan, bu sayıyla aralarında asal olan sayıları belirlemek oldukça basittir.
100'e Kadar En Büyük Asal Sayı
Asal sayılar, yalnızca 1 ve kendisi dışında pozitif tam böleni olmayan sayılardır. Matematikte temel bir yer tutan bu sayılar, hem teorik hem de pratik alanlarda geniş bir kullanıma sahiptir. Bu içerikte, 100'e kadar olan asal sayılar ve özellikleri ele alınacaktır.
105 bir asal sayı mıdır?
Matematikte asal sayılar yalnızca 1 ve kendisiyle bölünebilen sayılar olarak tanımlanır. 105 sayısının bu kritere uyup uymadığını anlamak için bölenlerinin detaylı bir analizi gerekiyor.
1110 bir asal sayı mıdır?
1110 sayısının asal olup olmadığını belirlemek için temel matematik kurallarına başvurulabilir. Çift sayıların 2'ye bölünebilme özelliği, bu tür durumlarda hızlı bir çözüm sunar. Sayının son basamağındaki sıfır, bölünebilirlik testleri için açık bir ipucu sağlar.
120'ye kadar olan asal sayılar nelerdir?
Matematik dünyasının yapı taşları olan asal sayılar, 120'ye kadar uzanan bir listede karşımıza çıkıyor. Yalnızca kendisine ve 1'e bölünebilen bu özel sayılar, hem temel matematik eğitiminde hem de ileri düzey uygulamalarda kritik bir rol oynuyor. Aşağıda, bu sayıların tam listesini ve dikkat çeken özelliklerini bulacaksınız.
121 asal mıdır?
121 sayısının asal olup olmadığını anlamak için temel matematik kurallarına başvurmak yeterli. Asal sayıların tanımından yola çıkarak bu sayının çarpanlarını incelemek, doğru sonuca ulaşmayı sağlıyor.
197 bir asal sayı mıdır?
197'nin asal sayı olup olmadığını belirlemek için matematiksel bir kontrol süreci izlenir. Bu süreçte sayının kareköküne kadar olan asal çarpanlara bölünüp bölünmediği incelenir ve sonuç net bir şekilde ortaya konur.
1'den 1000'e Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır ve matematikte önemli bir yere sahiptirler. Bu yazıda, 1'den 1000'e kadar olan asal sayıların listesi, özellikleri ve matematiksel önemi ele alınmaktadır. Asal sayılar, sayı teorisi ve kriptografi gibi alanlarda kritik bir rol oynar.
1'den 1000'e kadar kaç asal sayı vardır?
Matematikte asal sayılar, yalnızca 1 ve kendisiyle bölünebilen 1'den büyük tam sayılar olarak tanımlanır. 1'den 1000'e kadar olan aralıkta bu özelliği taşıyan sayıların belirlenmesi, Eratosthenes Kalburu gibi klasik yöntemlerle veya modern algoritmalarla mümkündür. Bu yöntemlerin uygulanması sonucunda, bahsi geçen aralıkta toplam 168 asal sayı bulunduğu ortaya çıkar.
1'den 100'e kadar kaç asal sayı vardır?
Matematiğin temel yapı taşları olan asal sayılar, 1'den 100'e kadar olan aralıkta belirli bir düzen içinde sıralanır. Bu özel sayı kümesi, yalnızca kendisi ve 1'e bölünebilme özelliğiyle diğer sayılardan ayrışır. İlk yüzlük sayı içindeki asal sayıların listesi ve temel özellikleri, sayılar teorisine giriş niteliği taşır.
1'den 100'e kadar olan asal sayılar nelerdir?
Matematikte özel bir yere sahip olan asal sayılar, sadece kendisi ve 1'e bölünebilen sayılardan oluşur. 1'den 100'e kadar olan bu özel sayıların tam listesi ve temel özellikleri aşağıda sunulmuştur.
1'den 10'a Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Matematikte önemli bir yere sahip olan asal sayılar, çeşitli uygulamalarda ve teorik çalışmalarda kritik rol oynamaktadır. 1'den 10'a kadar olan asal sayılar ve özellikleri detaylı bir şekilde ele alınmaktadır.
1'den 200'e kadar olan asal sayılar nelerdir?
Matematikte özel bir yere sahip olan asal sayılar, yalnızca 1 ve kendisiyle bölünebilen sayılardan oluşur. 1'den 200'e kadar olan bu özel sayıların tam listesi ve dikkat çekici özellikleri aşağıda sıralanmıştır.
1'den 20'e Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam böleni olan doğal sayılardır. Matematikte önemli bir yere sahip olan bu sayılar, sayılar teorisinin temel taşlarını oluşturur. Bu içerik, 1'den 20'ye kadar olan asal sayıları ve bu sayıların özelliklerini incelemektedir.
1'den 20'ye kadar olan asal sayılar nelerdir?
Matematiğin temel yapı taşlarından olan asal sayılar, 1'den 20'ye kadar olan aralıkta sekiz adettir. Bu özel sayı kümesi, yalnızca kendisi ve 1'e bölünebilme özelliğiyle diğer sayılardan ayrışır.
1'den 30'a Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Matematikte önemli bir yer tutan bu sayılar, çeşitli alanlarda geniş uygulamalara sahiptir. Bu yazıda, 1'den 30'a kadar olan asal sayılar ve özellikleri ele alınacaktır.
1'den 30'a kadar olan asal sayılar nelerdir?
Matematiğin temel yapı taşlarından olan asal sayılar, 1'den 30'a kadar olan aralıkta belirli bir düzen içinde sıralanır. Bu özel sayı kümesi, yalnızca kendisi ve 1'e bölünebilme özelliğiyle diğer sayılardan ayrışır.
1'den 40'a Kadar Asal Sayılar
Bu makalede, 1'den 40'a kadar olan asal sayılar incelenmektedir. Asal sayılar, yalnızca 1 ve kendisi ile tam bölünebilen doğal sayılardır. Matematikte önemli bir yere sahip olan bu sayılar, çeşitli özellikleri ve uygulamaları ile dikkat çekmektedir. Asal sayıların temel özellikleri ve matematikteki önemi ele alınmaktadır.
1'den 50'ye Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Bu yazıda, 1'den 50'ye kadar olan asal sayılar ile bu sayıların özellikleri ve farklı kullanım alanları detaylı olarak ele alınmaktadır. Matematikteki önemleri ve uygulama alanları vurgulanmaktadır.
1'den 60'a Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olan pozitif bölenleriyle tanımlanan doğal sayılardır. 1'den 60'a kadar olan asal sayılar, matematikte önemli bir yer tutar ve birçok uygulama alanında kritik bir rol oynar. Bu yazıda, bu asal sayıların özellikleri ve kullanım alanlarına odaklanılacaktır.
1'den 70'e Kadar Asal Sayılar
Bu içerik, 1'den 70'e kadar olan asal sayıları ve bu sayıların matematikteki önemini ele almaktadır. Asal sayıların tanımı, özellikleri, kullanım alanları ve ilginç bilgilerle birlikte, matematiksel düşünceyi geliştirmek için temel bir kaynak sunmaktadır.
1'den 80'e Kadar Asal Sayılar
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan sayılardır. Bu yazıda, 1'den 80'e kadar olan asal sayılar listelenmiş ve bu sayıların matematikteki önemi ile pratik uygulamaları ele alınmıştır. Asal sayılar, sayılar teorisinin temel taşlarını oluşturur.
1'den 90'a Kadar Asal Sayılar
Asal sayılar, matematiğin temel taşları arasında yer alır ve sadece 1 ile kendisi olmak üzere iki tam böleni bulunan pozitif tam sayılardır. Bu yazıda, 1'den 90'a kadar olan asal sayılar, özellikleri, tarihçesi ve uygulamaları detaylı bir şekilde ele alınacaktır.
1'den büyük, sadece 1 ve kendisiyle bölünebilen doğal sayılara ne denir?
Matematik dünyasının temel yapı taşları olan asal sayılar, yalnızca 1 ve kendisiyle bölünebilen doğal sayılar olarak tanımlanır. Bu benzersiz sayı kümesi, sayılar teorisinden modern şifrelemeye kadar birçok alanda hayati rol oynayan özelliklere sahiptir.
2 ile aralarında asal olmak ne anlama gelir?
İki sayının 1'den başka ortak böleni olmaması durumu, aralarında asallık kavramını tanımlar. Bu yazıda, özellikle 2 sayısı ile diğer sayıların aralarında asal olma koşulu incelenmektedir.
2 ve 0 aralarında asal mıdır?
Matematikte aralarında asallık kavramı, pozitif tam sayılar için tanımlanmıştır. Sıfır sayısının özel durumu, bu tanımın dışında kalır ve ortak bölen analizi gerektirir. İki sayının aralarında asal olabilmesi için en büyük ortak bölenlerinin 1 olması şartı aranır.
229 sayısı asal mıdır?
229 sayısının asal olup olmadığını belirlemek için temel matematiksel yöntemlerle yapılan sistematik bir inceleme sunuluyor. Sayının bölenleri kontrol edilerek asallık kriterleri adım adım değerlendiriliyor ve sonuç net bir şekilde ortaya konuyor.
23 bir asal sayı mıdır?
23 sayısının asal olup olmadığı, matematikte sıkça merak edilen bir konudur. Bu sayının bölenleri incelendiğinde, yalnızca kendisine ve bire tam bölündüğü görülür, bu da onu asal sayılar arasında yer alan bir değer yapar.
23 sayısı asal mıdır?
Matematikte asal sayılar, yalnızca 1 ve kendisiyle bölünebilen sayılar olarak tanımlanır. 23 sayısının bu kriteri nasıl karşıladığını ve neden asal olduğunu inceleyelim.
27 ve 81 aralarında asal mıdır?
İki sayının aralarında asal olup olmadığını belirlemek için en büyük ortak bölenlerinin 1 olması gerektiği temel kuralından hareketle, 27 ve 81 sayılarının durumu inceleniyor. Bu sayıların asal çarpanlarına ayrılması ve ortak bölenlerinin belirlenmesi, aralarında asal olmadıklarını gösteriyor.
3 ve 9 aralarında asal mıdır?
İki sayının aralarında asal olup olmadığını belirlemek için ortak bölenlerini incelemek gerekir. Ortak bölenleri yalnızca 1 ise bu sayılar aralarında asal kabul edilir.
32 bir asal sayı mıdır?
32 sayısının asal olup olmadığı merak edilen bir konudur. Asal sayıların tanımı ve 32'nin matematiksel özellikleri incelendiğinde, bu sayının neden asal sayılar arasında yer almadığı netlik kazanır.
4 ile 6 aralarında asal mıdır?
Ortak bölen kavramı üzerinden ilerleyerek, iki sayının aralarında asal olup olmadığını belirlemek için temel bir matematiksel yaklaşım sunuluyor. Bu inceleme, sayıların bölenlerini ve ortak özelliklerini analiz ederek sonuca ulaşmayı hedefliyor.
4 ve 1 aralarında asal mıdır?
İki sayının aralarında asal olup olmadığını belirlemek için ortak bölenlerini ve en büyük ortak bölenini incelemek gerekir. Bu durumda, 4 ve 1 sayılarının ortak bölenleri yalnızca 1 olduğundan, aralarında asal oldukları sonucuna varılır.
40 ile 1 aralarında asal mıdır?
Matematikte aralarında asal sayılar kavramı, sayıların ortak bölenlerinin yalnızca 1 olması durumunu ifade eder. 40 ve 1 sayılarının bu özelliği taşıyıp taşımadığını belirlemek için ortak bölenleri ve EBOB değeri incelenir.
51 ve 16 aralarında asal mıdır?
İki sayının aralarında asal olup olmadığını belirlemek için ortak bölenlerini ve en büyük ortak bölenini incelemek gerekir. Bu durumda, 51 ve 16 sayılarının bölenleri ve asal çarpanları üzerinden bir analiz yapılarak sonuca ulaşılabilir.
59 sayısı asal mıdır?
59 sayısının asal sayı olup olmadığını belirlemek için sistematik bir kontrol yapılıyor. Sayının kareköküne kadar olan asal bölenlerle bölünebilirliği inceleniyor ve her adımda neden bölünmediği açıklanıyor.
6 bir asal sayı mıdır?
Matematikte asal sayılar yalnızca 1 ve kendisiyle bölünebilen sayılar olarak tanımlanır. Bu tanım ışığında 6 sayısının asal olup olmadığı, bölenleri incelenerek netlik kazanıyor. Sayının çarpanlarına ayrılma durumu, asallık kriterlerini karşılayıp karşılamadığını ortaya koyuyor.
61 bir asal sayı mıdır?
61 sayısının asal olup olmadığını belirlemek için yapılan matematiksel kontroller, bu sayının yalnızca 1 ve kendisi tarafından bölünebildiğini gösteriyor. 2'den 7'ye kadar olan asal sayılarla yapılan bölme işlemleri, 61'in bu sayıların hiçbirine tam bölünmediğini kanıtlıyor.
63 bir asal sayı mıdır?
63 sayısının asal sayı tanımına uygun olup olmadığını belirlemek için bölenleri inceleniyor. Yalnızca 1 ve kendisiyle bölünebilme koşulunu sağlamayan 63'ün, birden fazla çarpanı olduğu görülüyor. Bu durum, sayının asal olmadığını ve bileşik sayılar sınıfında yer aldığını gösteriyor.
8 ve 15 aralarında asal mıdır?
Matematikte aralarında asal sayılar, ortak bölenleri sadece 1 olan pozitif tam sayılar olarak tanımlanır. Bu kavram, sayıların asal çarpanlarına ayrılarak veya en büyük ortak bölenlerinin hesaplanmasıyla kolayca anlaşılabilir. Örneğin, 8 ve 15 sayılarının durumu bu ilişkiyi net bir şekilde gösterir.
80'e kadar olan asal sayılar nelerdir?
Matematikte özel bir yeri olan asal sayılar, yalnızca kendisine ve 1'e bölünebilen sayılardır. Bu yazıda 80'e kadar olan asal sayıların listesi, toplam adedi ve temel özellikleri ele alınmaktadır.
9 ile 4 aralarında asal mıdır?
İki sayının aralarında asal olup olmadığını belirlemek için ortak bölenlerini incelemek gerekir. Bu durumda, 9 ve 4'ün bölenleri karşılaştırılarak ortak bölenlerinin yalnızca 1 olduğu görülür.
98 asal sayı mıdır?
98 sayısının asal olup olmadığı merak edilen bir matematik sorusudur. Bu konu, asal sayı tanımı ve bölen analizi üzerinden detaylı şekilde incelenmektedir.
99'a kadar olan asal sayılar nelerdir?
Matematik dünyasının temel yapı taşları olan asal sayılar, 1'den büyük ve yalnızca kendisi ile 1'e bölünebilen sayılardır. 99'a kadar olan bu özel sayıların listesi ve temel özellikleri aşağıda sunulmuştur.
Aralarında Asal Sayılar Nasıl Bulunur?
Bu içerik, asal sayıların tanımı, özellikleri ve bunları bulma yöntemleri üzerine kapsamlı bir inceleme sunmaktadır. Asal sayıların matematikteki önemi ve farklı yöntemler aracılığıyla nasıl belirlendiğine dair detaylı bilgiler verilmektedir. Ayrıca, asal sayıların modern teknolojideki uygulamalarına da değinilmektedir.
Ardışık iki doğal sayı aralarında asal mıdır?
Ardışık doğal sayıların ortak bölenlerini inceleyen bu matematiksel ilişki, sayıların temel özelliklerinden kaynaklanan zarif bir sonuç sunuyor. İki ardışık tam sayının her zaman 1'den büyük ortak böleni olmadığı, bu sayıların aralarında asal olmasını sağlayan mantıksal bir çerçeveyle açıklanıyor.
Asal sayı kalburu nasıl çalışır?
Eratosthenes Kalburu olarak bilinen bu antik yöntem, belirli bir limit dahilindeki tüm asal sayıları sistematik şekilde bulmak için kullanılan zarif bir algoritmadır. Küçük asal sayıların katlarını eleyerek çalışan bu teknik, hem matematiksel mantığı anlamak hem de sayılar teorisine giriş yapmak için ideal bir araç sunar.
Asal sayılar hangi sayıdan itibaren başlar?
Matematik dünyasının bu özel sayıları, yalnızca kendisi ve 1'e bölünebilme özelliğiyle diğer tam sayılardan ayrılır. En küçük asal sayı olan 2'den başlayarak sonsuz bir diziyi oluştururlar ve sayılar teorisinde temel bir rol oynarlar.
Bir sayının asal çarpan sayısı nasıl hesaplanır?
Matematikte bir sayının asal çarpan sayısını bulmak, sayı teorisinin temel konularından biridir. Bu yöntem, bir sayının farklı asal bölenlerini belirleyerek sayının yapısını anlamamıza yardımcı olur. İster 12 gibi küçük sayılar olsun, ister büyük sayılar için uygulansın, adımları takip etmek kesin sonuçlar verir.
Bir sayının asal çarpanları nasıl bulunur?
Matematikte bir sayıyı oluşturan temel yapı taşlarını keşfetmek için kullanılan asal çarpan bulma teknikleri, hem temel aritmetik hem de ileri düzey problem çözümlerinde önemli bir yer tutar.
Bir sayının asal çarpanlarının toplamı nasıl hesaplanır?
Matematikte bir sayının asal çarpanlarını bulmak ve bu çarpanların toplamını hesaplamak, sayılar teorisinin temel konularından biridir. Bu işlem, bir sayının yapı taşlarını ortaya çıkarmak ve bu asal bileşenlerin toplam değerini belirlemek için kullanılır. Aşağıdaki rehber, bu sürecin adım adım nasıl ilerlediğini ve pratik örneklerle nasıl uygulandığını açıklamaktadır.
En büyük asal sayı var mıdır? en küçük asal sayı kaçtır?
Asal sayıların gizemli dünyası, matematik tarihinin en temel ve büyüleyici sorularından birini barındırıyor. Sonsuzluk kavramıyla iç içe geçen bu sayıların sınırlarını anlamak, Öklid'den günümüze uzanan bir keşif yolculuğunu temsil ederken, en küçük asal olan 2'nin özellikleri de sayı teorisinin yapı taşlarını oluşturuyor.
Her doğal sayı asal çarpanlara ayrılabilir mi?
Matematikteki en temel ve önemli teoremlerden biri olan Aritmetiğin Temel Teoremi, doğal sayıların yapısal özelliklerini ortaya koyar. Bu teorem, 1'den büyük tüm doğal sayıların asal çarpanlara nasıl ayrıştırılabileceğini ve bu ayrıştırmanın neden benzersiz olduğunu açıklar.
İki tek sayı her zaman aralarında asal mıdır?
Tek sayıların aralarında asal olma durumu, sayıların yalnızca tek olmasıyla doğrudan ilişkili değildir. Ortak bölenlerin varlığı, bu ilişkiyi belirleyen temel faktördür ve çeşitli örneklerle bu durum netleşir.
Neon bir asal gaz mıdır?
Periyodik tablonun 18. grubunda yer alan neon, kararlı elektron konfigürasyonu ve düşük kimyasal reaktivitesiyle tipik bir asal gaz özelliği sergiler. Renksiz ve kokusuz olan bu element, özellikle neon lambalardaki ışık yayma özelliğiyle tanınır.
Sıfır ile bir sayı aralarında asal mıdır?
Sıfırın matematiksel özellikleri, onun diğer sayılarla aralarında asal olma durumunu belirlerken dikkatle incelenmelidir. Aralarında asallık kavramının pozitif tam sayılar için tanımlandığı ve sıfırın bu kapsamda neden değerlendirilemeyeceği, sayılar teorisindeki temel kurallar ışığında açıklanmaktadır.
